Outils pour utilisateurs
Table des matières
Objectifs pédagogiques de l'activité
- découvrir le codage ou utiliser le codage pour créer des objets 3D
- manipuler un langage informatique et avoir les analogies avec les autres langages humains
- utiliser un logiciel de création 3D qui mets à profit les apprentissages théoriques appris en collège (géométrie, trigonométrie)
- analyser un objet complexe et le décomposer en sous-objets plus simples
- réaliser la modélisation d'un objet réel en code informatique (texte)
- en savoir plus sur l'impression 3D et visiter un acteur de l'impression 3D du territoire roubaisien (entreprise Dagoma qui fabrique des imprimantes 3D ou le Fablab de Lille (Rue des Arts, friche Roussel) qui peut vous guider ou vous accompagner pour vos projets 3D.
Durée de l'activité
plusieurs séances (au moins 4) de deux heures chacune
Nombres de participants maximum
10 / 12 personnes, idéalement des binômes parent/enfant
Tranche d'âge du public (âge minimum)
à partir de 13 ans jusqu'à 107 ans (notions de trigonométrie (angles, ¶, sinus, cosinus) acquises)
Pré-requis
→ savoir écrire, compter
→ connaître les angles, les sinus et cosinus (trigonométrie)
Matériel nécessaire durant l'activité
Matériel nécessaire et mis à disposition des participants: ordinateur, logiciel Openscad, imprimantes 3D et accessoires, logiciel Cura
Déroulement de l'activité
Coder et imprimer un objet 3D
Le but de cet atelier est:
- d'analyser l'objet à coder et de penser un scenario de création de sous-objets
- de décomposer l'objet en sous-objets emboîtables et imprimables par une imprimante 3D
- de lister les dimensions des sous-objets en insistant sur les emboîtements et en utilisant des variables
- de programmer les sous-objets avec OpenScad
- de produire des fichiers compatibles avec les imprimantes 3d
- de finaliser les objets (mise à l'échelle,finition)
- d'imprimer des sous-objets, de vérifier leur compatibilité et d'ajuster les dimensions
Analyser l'objet à coder
Vous avez 15 ans ou presque, vous réfléchissez à l'orientation que vous choisirez et pour affiner votre choix, vous avez décidez de trouver un stage dans des entreprises dont l'activité vous intéresse.
Çà y est, vous avez décrochez un stage dans une entreprise informatique et le sujet de votre stage est le suivant:
“Pour répondre aux souhaits de nos adhérents, l'association vous propose de l'aider à concevoir et produire un arbre généalogique modulaire 3D. A partir d'un point d'origine, les modules que vous proposerez permettront de construire une arborescence contenant l'ensemble des descendants d'un couple.
Pour représenter les descendants d'un ancêtre né pendant la révolution française (1795-1811), il est fort probable qu'il faille envisager une représentation contenant près de 1000 descendants. Il faut y ajouter les conjoints des couples de parents … cela ajoutera près de 1000 personnes supplémentaires.
Génération n ou niveau n : chaque enfant de la génération n-1 pourra avoir de 1 à 15 enfants
Génération 4 ou niveau 4 : chaque enfant de la génération 3 pourra avoir de 1 à 15 enfants
Génération 3 ou niveau 3 : chaque enfant de la génération 2 pourra avoir de 1 à 15 enfants
Génération 2 ou niveau 2 : 1 à 15 enfants
Génération 1 ou niveau 1 : 2 personnes
Représenter cet arbre descendant sur un plan se révèle impossible à moins de disposer d'un … très grand mur.
Comme le poumon des mammifères pour augmenter sa surface d'échange air/sang ou l'arbre pour augmenter sa surface d'exposition au soleil pour la photosynthèse, nous tenterons une représentation en 3D et disposer ainsi de la place nécessaire pour contenir et hiérarchiser.
Ce qui vous est demandé ici est donc de proposer une représentation 3D de l'arbre.
Et si nous proposions la production d'un arbre de type mécano. L'arbre part d'un tronc (qui ne fait pas partie de l'exercice, on pourra se servir avec avantage d'un pied pupitre de musicien). Nous débuterons le travail par le haut du fût du tronc où seront représentés les deux individus du couple du début de 19ème siècle d'où partirons un nombre de 1 à 15 enfants (1ère subdivision).
De ce premier plan de subdivisions partiront donc un nombre variable de branches de première génération qui elles-même se subdiviseront à leur tour en un nombre variable de branches de seconde génération et ainsi de suite.
Inspirons d'exemples présents dans la nature (les arbres) ou dans notre corps (nos bronches) pour nous aider à comprendre comment nous pourrons résoudre ce défi.

Nous pouvons observer ici un arbre dont chaque branche donne naissance à un nombre variable de branches sur plusieurs générations.
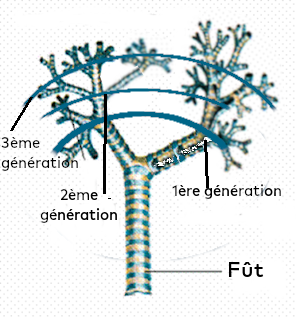
Si nous examinons cet arbre présent dans nos bronches, nous voyons qu'à chaque subdivision ou génération, par un nombre variable de branches et que cela se répète à chaque subdivision suivante.
L'arbre généalogique de nos ancêtre obéit au même phénomène: chacun de nos ancêtres à un nombre variable d'enfants et cela se répète à chaque génération !
Il est difficile voire impossible de représenter une telle structure sur un plan (2 dimensions) au-delà de la troisième génération.
La représentation en 3 dimensions devra résoudre cette difficulté de représentation.
Je vous propose donc de concevoir un arbre en trois dimensions avec un nombre variable de branches à chaque génération et de modéliser les sous-objets emboîtables de cet arbre en les imprimant sur une imprimante 3D classique.
Différents sous-objets de notre arbre:
- le tronc: comme annoncé, nous n'imprimerons pas le tronc, un pied de pupitre de musicien fera très bien notre affaire.
- les branches: du tronc partent un nombre variables de branches. Comme pour l'arbre réel illustré plus haut, nous déciderons que certaines branches sont inclinées à 30 degrés et d'autres à 50 degrés.
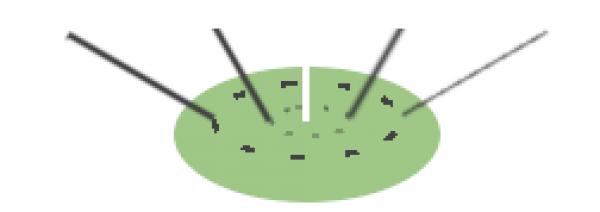
- pour emboîter les sous-branches aux branches, nous nous servirons d'un capitule (comme le capitule d'une fleur) d'où partent nos branches filles à leur tour inclinées à 30 degrés et où à 50 degrés.
Sous-ensembles le l'arbre 3D
Pour pouvoir modéliser toute forme d'arborescence en fonction des besoins (nombre variable d'enfants dans chaque famille), il faudra être capable de la composer au montage en fonction des besoins spécifiques.
Par conséquent, pour relier les branches filles à leur branche mère, nous créerons des couronnes à deux plateaux superposés qui termineront chaque branche mère.
Pour cela, nous proposons les sous-ensembles emboîtables suivants:
- les branches (A),
- les capitules (B),
- les raccords entre les capitules et les branches (C),
- raccord tronc / couronne de l'arbre (D),
- des feuilles pour afficher les textes avec les noms et détails des descendants présents dans l'arbre.
Caractéristiques de la branche
 La branche (A) sera le composant les plus facile à programmer.
La branche (A) sera le composant les plus facile à programmer.
Elle aura une longueur fixe et qui pourra changer de valeur pendant les tests.
Elle sera cylindrique et terminée à chaque extrémité pour une forme polygonale; cela évitera la rotation des branches autour de leur axe.
- nous désignerons la longueur par les variables di_br et lg_br à laquelle nous donnerons une valeur initiale de 170 mm hors tout (cad embouts compris / lg_br=170).
- elle sera cylindrique d'un diamètre de 10 mm (di_br=10)
- elle sera prolongée d'un embout cylindrique hexagonal (cylindre à 6 côtés sur sa longueur) qui pourra s'enfoncer dans le capitule à l'une de ses extrémité (voir haut_cap=ep_grdplatcap+ep_ptplatcap+ep_anncap : attention à l'inclinaison) et dans le raccord à l'autre extrémité (le diamètre de l'embout sera de 1.5 mm plus petit que celui de la branche).
Résumé:
// variables utilisées
//dimensions communes
facettes=6;
// dimensions branche
di_br=10; // diamètre branche
lg_emboutsbr=15; // longueur des embouts des branches
lg_br=170; // longueur de la branche (hors tout)
//
//dimensions capitule
di_grdplatcap=150; // diamètre plateau supérieur du capitule
ep_grdplatcap=2; // épaisseur plateau supérieur du capitule
di_ptplatcap=90; // diamètre plateau inférieur du capitule
ep_ptplatcap=2; // épaisseur plateau inférieur du capitule
ep_anncap=14; // épaisseur anneau inter plateaux du capitule
//
//dimensions socle
di_socle=15; // diamètre du socle (à adapter au support
// choisi (pied de pupitre de musicien
// par exemple)
//dimensions calculées
haut_cap=ep_grdplatcap+ep_ptplatcap+ep_anncap;
di_emboutsbr=di_br-1.0; // diamètre des embouts
Langage Openscad
Pour la création de ce sous objet, nous découvrirons le langage Openscad, la syntaxe des commandes, les variables et les variables spéciales et les principes de programmation avec ce langage. Nous n'utiliserons que deux fonctions: une fonction 3D cylinder() et une fonction de transformation translate().
Caractéristiques du capitule
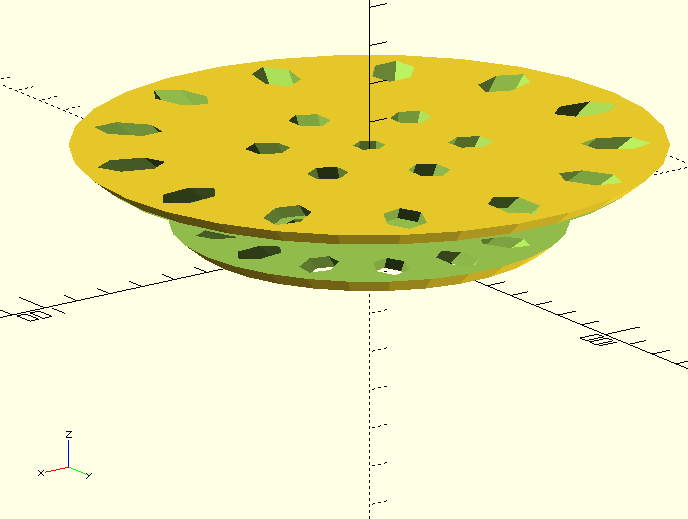 Le capitule est le composant le plus ardu à programmer.
Le capitule est le composant le plus ardu à programmer.
Il sera composé de deux plateaux concentriques circulaires superposés, posés horizontalement avec un intervalle.
Ils seront percés d'un nombre variable de trous pentagonaux disposés en deux cercles au tour du centre et dans lesquels les branches viendront s'insérer.
Pour percer les trous dans l'angle et la direction souhaitée, nous aurons ici besoin de calculer les coordonnées de chaque point à l'aide des sinus / cosinus de ces points:
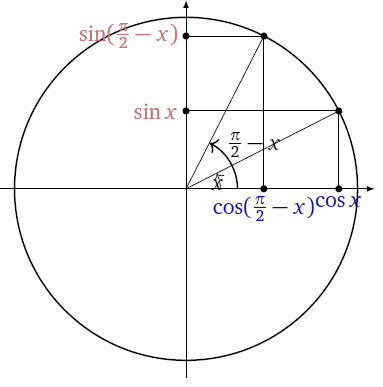
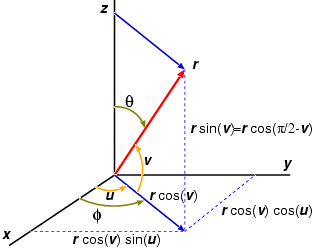
Résumé:
//dimensions communes facettes=6; // dimensions branche di_br=10; // diamètre branche lg_emboutsbr=15; // longueur des embouts lg_br=170; // longueur de la branche // //dimensions capitule di_grdplatcap=150; // diamètre plateau supérieur du capitule ep_grdplatcap=3; // épaisseur plateau supérieur du capitule di_ptplatcap=90; // diamètre plateau inférieur du capitule ep_ptplatcap=4; // épaisseur plateau inférieur du capitule ep_anncap=14; // épaisseur anneau inter plateaux du capitule //
Caractéristiques du raccord capitule / branches
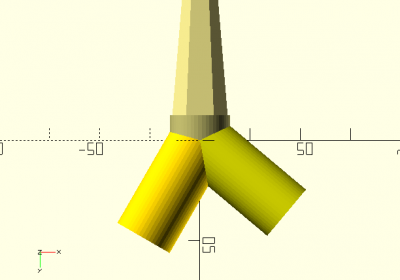
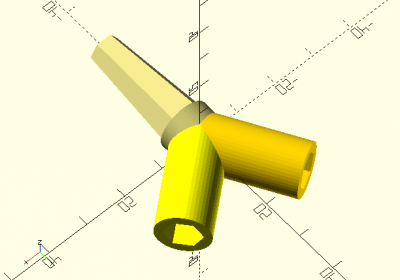
La troisième pièce de notre montage aura le rôle crucial de cheviller le capitule à la branche qui le supporte. Il aura la forme d'un Y irrégulier
- un axe plein montant vertical qui supportera les différents éléments du capitule
- deux axes creux descendants qui accueilleront une branche quittant un capitule à 50° ou une branche quittant un capitule à 30°.
toutes les variables:
//dimensions communes facettes=6; // dimensions branche di_br=10; // diamètre branche lg_emboutsbr=15; // longueur des embouts lg_br=170; // longueur de la branche // //dimensions capitule di_grdplatcap=150; // diamètre plateau supérieur du capitule ep_grdplatcap=3; // épaisseur plateau supérieur du capitule di_ptplatcap=90; // diamètre plateau inférieur du capitule ep_ptplatcap=4; // épaisseur plateau inférieur du capitule ep_anncap=14; // épaisseur anneau inter plateaux du capitule // //dimensions calculées haut_cap=ep_grdplatcap+ep_ptplatcap+ep_anncap+3; //
Caractéristiques du raccord socle / couronne de l'arbre
La quatrième et dernière pièce de notre montage assurera la fixation de notre ensemble sur le pied que vous aurez choisi. On utilisera donc un seul raccord-socle pour un arbre.
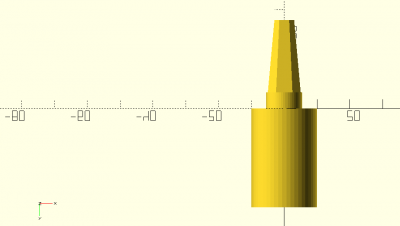
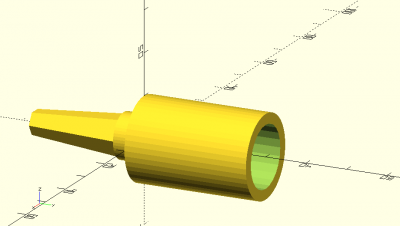 Ce raccord sera composé de:
Ce raccord sera composé de:
- un axe plein montant vertical qui supportera les différents éléments du capitule
- un axe creux descendant qui accueillera le piton sur support, ici un pupitre de musicien.
Résumé:
toutes les variables:
//dimensions communes facettes=6; // dimensions branche di_br=10; // diamètre branche lg_emboutsbr=15; // longueur des embouts lg_br=170; // longueur de la branche // //dimensions capitule di_grdplatcap=150; // diamètre plateau supérieur du capitule ep_grdplatcap=3; // épaisseur plateau supérieur du capitule di_ptplatcap=90; // diamètre plateau inférieur du capitule ep_ptplatcap=4; // épaisseur plateau inférieur du capitule ep_anncap=14; // épaisseur anneau inter plateaux du capitule // //dimensions calculées haut_cap=ep_grdplatcap+ep_ptplatcap+ep_anncap+3; //
Caractéristiques des feuilles
L'arborescence est faite pour représenter les descendants d'un ancêtre ou l'organisation d'une entreprise sous forme d'organigramme.
Pour afficher les personnes qui composent l'organigramme, il faudra pouvoir poser des étiquettes au différentes terminaisons et intersection des branches.
Et si nous utilisions des feuilles comme les feuilles de l'arbre.
de nombreuses formes de feuilles existent. Pour cet exercice, nous choisirons les feuilles de tilleul dont le forme est agréable à voir.
Comment s'y prendre ?
Coder une feuille d'arbre est possible mais représente un véritable défi. Nous arriver à nos fins, nous choisirons une photo de feuille de tilleul (de bonne résolution et téléchargée sur Wikimedia Commons) et à laquelle nous aurons préalablement ajouté un pétiole de belle longueur avec le logiciel libre GIMP.
Une photo est un document 2D … comment passer de la photo 2D à un document 3D modifiable avec Openscad.
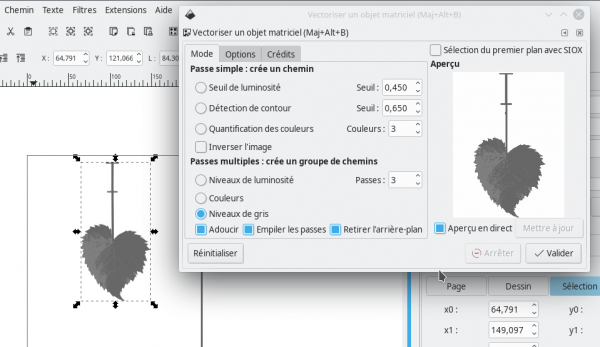
Cela est possible mais il faut d'abord passer notre photo d'image matricielle en image vectorielle et nous choisirons le logiciel libre de traitement d'images vectorielles Inkscape pour faire cela.

Le tutoriel en ligne Convert Any 2D Image to a 3D Object Using OpenSCAD (and Only Free Software) nous permettra d'aboutir facilement à la création d'une feuille de tilleul 3D avec Openscad. Voici quelques copie d'écran:
- Vectoriser une image 2D
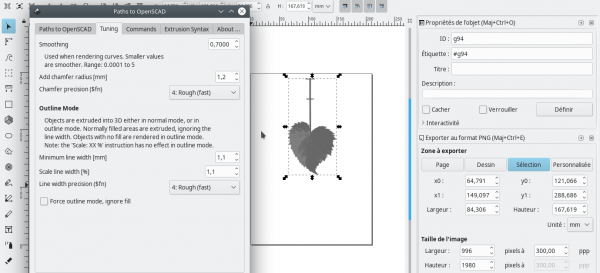
- Génération d'un script Openscad pour l'image vectorisée
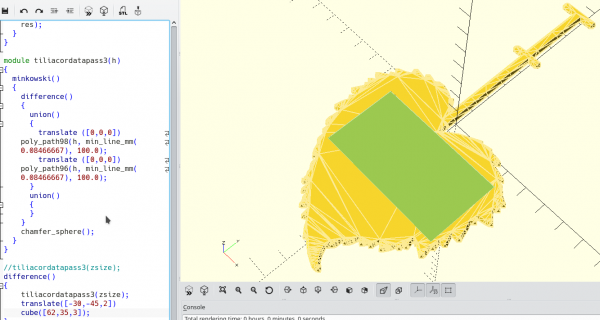
- Adaptation du script Openscad

Principales fonctions
Les principales fonctions qui seront utilisées au cours de cet atelier sont les les suivantes:
- cylinder(h,r1|d1,r2|d2,center) où h est la hauteur du cylindre, r ou d ses rayon/diamètre à chaque extrémité et center permet de positionner son axe par rapport au centre.
Les principales opérations que nous exécuterons seront:
- difference() cette opération permet de soustraire à la forme construite par la première fonction toutes les formes décrites par les fonctions suivantes.
Par exemple, le codetranslate([0,0,0]) { color("DarkKhaki"){ translate([0,-4,-diametre_branche/2]){ difference(){ cylinder(d=17.6,h=2.5,$fn=60); translate([0,0,0.001]) cylinder(d=14.8,h=2.6.001,$fn=6); } } } }creusera un cylindre hexagonal ($fn=6) de 14.8 mm de diamètre à l'intérieur d'un cylindre circulaire ($fn=60) de 17.6 mm de diamètre et de même hauteur.
Les principaux mouvements dont nous aurons besoin sont:
- translate([x,y,z]) permet de se déplacer du point en cours vers le point [x,y,z]
- rotation([x,y,z]) permet d'orienter les parties de l'objet en cours dans la direction de l'angle [x,y,z]
D'une manière générale, l'opération ou le mouvement peuvent ne concerner qu'une exécution de la fonction ou plusieurs.
du fichier à l'objet imprimé
Le processus de production d'un fichier 3D comporte 3 étapes essentielle:
- création du modèle avec un logiciel de codage (OpenScad), avec un modélisateur (Blender, ThinkerCad, …) ou encore en téléchargeant le fichier depuis un site (il s'agit alors d'une copie et non d'une création !)
- la transformation du fichier 3D et sa préparation pour l'imprimante (choix de la densité, de la taille, du positionnement sur le plateau de l'imprimante, de l'ajout de support pour les parties en suspension, etc
- l'impression proprement dite (qui peut être très, très longue pour les objets complexes
L'étape 1 part d'une feuille blanche pour arriver à un fichier STL, la seconde étape part du fichier STL (identique pour toutes les imprimantes) pour arriver à un fichier Gcode (spécifique à un objet pour un modèle d'imprimante) et la dernière consiste à copier le fichier Gcode sur une carte SD qui sera introduite dans l'imprimante pour lancer l'impression.

du bon usage des bibliothèques d'objets
Comme pour les images numériques, Internet propose un nombre illimité d'objet STL à imprimer. Si on écarte d'impression d'objets “gadget” pour lesquels l'acquisition d'une imprimante 3D parait inappropriée, ces bibliothèques proposent d'autres ressources.
- des fichiers OpenScad personnalisables
- des contacts avec des créateurs souvent très érudits
A titre d'exemple, je vous propose de cliquer sur ce lien pour voir voir que ces bibliothèques proposent aussi des codes OpenScad pour des objets … alors facilement “customisables” …